他人を褒めるということ
アメリカで学んだことで最も良かったのはなんだろうかと考えている。
実験技術やプログラミングなど、学んだことは多々あるが、どんな他人でも存在を認める態度(少なくとも認めたふりをすること)、そして他人をちゃんと褒めるという態度は自分の生活に少なからぬ良い影響を与えてくれたように思える。まあ建前で褒めているってのもあるんだろうけど、少なくとも互いにポジティブな表現で会話するとコミュニケーションが円滑になる。
他人の存在を承認することを前提として、そこからコミュニケーションを行うというボスやラボの皆の態度は、自分の中で他者と付き合うための新しい標準になってしまっている。もちろん批判をすることもあるけれど、それは科学的な議論の内容についてであって、存在の是非についてではない。聴き逃してる部分もあるとは思うが。
30超えても人生観がどんどん変わっていくんだなと思うし、そういう出会いがあったことに感謝したいなと思う。
あとはこの恩返しとして自分の下の世代をしっかり褒めていけるような機会があるといいんだけど。
MoldenをMac OS Sierraにインストールした
自分のPC上でも分子構造や動力学シミュレーションの結果を見たいと思い、Moldenをインストールした。VMDを使った時は分子の結合開裂や結合形成が表現できてなかったのでこっちのほうが好きである。
Moldenは公式サイトから入手
How to get a copy of Molden
公式サイトに従って
tar -xvf molden5.7.tar
cd molden5.7
vi makefile
で解凍してmakeしようとしたのだが、エラーが出て止まる。
コンパイラの問題っぽい。
makefileのコメント
# with GCC4.0 or higher replace the line with:
# 'external gfortran_iargc'
に従ってmolden.fを書き換えて
xcode-select --install
で開発ツールをインストールしたら上手く行った。
基底関数雑感2
カルボカチオンの出て来る系を扱っている。
モデルを使ったCCSD(T)/aug-cc-pVTZのエネルギーとの比較ではM06HF/def2-SVPPが最もコストパフォーマンスの良い汎関数/基底関数であることがわかったのだが、これまでにAhlrichの基底系をしっかり試したことがないのでいまひとつピンとこない。超共役による結合の伸長や結合角の変化をしっかり表現できるか気になる。
元文献(http://pubs.rsc.org/en/Content/ArticleLanding/2005/CP/b508541a#!divAbstract)を読む限りではdef2-SVPPなら炭素にもプロトンにも分極関数がしっかり入ってるので大丈夫な気がするのだが、不安が残る。
そこでエチルカチオンをモデルとして基底関数をチェックした。
使用した汎関数はB3LYP。基底関数はSTO-3G, 6-31G, 6-31G*, 6-31G**, 6-311+G(2df,2p), SV, def2-SV, def2-SVP, def2-SVPPの9種。気相中での構造最適化を行った。
小さい基底関数であるSTO-3G, 6-31G, SVではCS対称な構造が、それ以外ではC2V対称性のある橋架け構造が得られた。結合長は以下の通り。
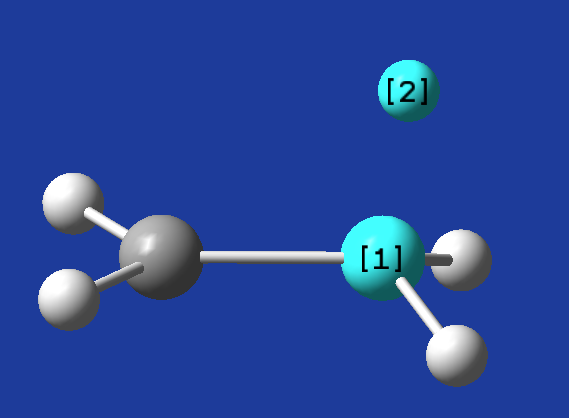
Fig 1. STO-3G, 6-31G, SVで得られた構造
結合長[1]-[2]
STO-3G: 1.15Å
6-31G: 1.14Å
SV: 1.15 Å

FIG 2. その他で得られた構造
結合長[1]-[2]
6-31G*: 1.32Å
6-31G**: 1.32 Å
6-311+G(2df,2p): 1.32 Å
def2-SV: 1.33 Å
def2-SVP: 1.32 Å
def2-SVPP: 1.33 Å
流石に小さい基底系を使うと非古典的な構造を表現できない。しかし結合の伸長を結構表現できていて驚いた。炭素に分極関数を付与すれば水素上の分極関数の有無によらずきちんと非古典的カルボカチオンを表現できる。また、分極関数のあるものについては、結合長を見る限りでは構造の表現に関してはほとんど変わらない。構造最適化に使う基底系として6-31G*が推奨されるのも納得がいく。構造が近いのであれば、反応前後のエネルギー差をしっかり記述できる基底関数を利用して信頼に値する計算ができる。
アパートを退去した
7月いっぱいでアパートの契約が切れたため、退去した。
確か5月ころに去る予定である旨を通告した。退去当日は、管理人が部屋の中を見ることもなく、単純に鍵を渡してdepositの返却先の住所を教えて手続きは完了である。とりあえず口頭ではあるが、部屋が雨漏りなどで壊れた部分は直す責任がないことを確認しておいた。まだこの地にいると言っておいたので、depositをそれほど無茶には使わないだろうと期待している。
家具類は捨てることにした。売るのが面倒くさいしどうせ中古の安物だからそれぞれ10ドルにもならないだろうと思い、ゴミ捨て場にそのまま置いていった。いくつかは誰かがすぐさま持っていってくれた。ボロいけど、なんだかんだで愛着がある家具類なので、誰かが使ってくれるのは嬉しいものであるなと思った。
この地に来てからずっと住んでいたアパートなので去るのは寂しい感じがする。しかしながら、これまでに計7回(短期の留学含めるともっと増える)引っ越したが、その全てで寂しさを感じていたので場所を移るという行為自体があまり好きじゃないんだろうと思う。
だが、今みたいに場所を転々として暮らしていると、自分が愛着を持つ、第二、第三の故郷が年々増えていく。これは幸せなことなんだろうと思った。
ラボのサーバーにPython3を入れた
先日作ったプログラムをボスが使いたいので使い方教えれ、とのことになった。
残念なことに、このラボには自分以外Pythonユーザーがいないので、折角プログラムを皆に配布しても各自環境構築しないと使えない。
だったらラボのサーバー上で使えば楽じゃないかと思い立ったが、ラボのサーバーのPythonは2.6で止まっているため、Python3のコードは走らない。そこで自分がサーバーのPython環境を構築することになった。
四苦八苦しながら2時間かけてインストールしたので、備忘録として残しておきたい。
OSは Red Hat Enterprise Linux Server release 6.9 (Santiago)。当然だが、今まで自分が使ってたMacOSシリーズとはちょっと違っており、bashでaptと叩いても動かない。困る。代わりにyumを使わないとならないらしい。yum使うのは多分初めて。厳しい。
基本的には以下のサイトに従った。
https://www.digitalocean.com/community/tutorials/how-to-install-python-3-and-set-up-a-local-programming-environment-on-centos-7
また、他にも
$ yum install -y zlib-devel bzip2-devel openssl-devel ncurses-devel sqlite-devel readline-devel tk-devel
で関連する道具を集めて、
更に
sudo yum -y install https://dl.fedoraproject.org/pub/epel/epel-release-latest-6.noarch.rpm sudo yum -y install https://rhel6.iuscommunity.org/ius-release.rpm
でIUS更新とかして、
上記の組み合わせでやっとpip3.6が動いた。
しかし、
pip3.6 install numpy scipy
でnumpyとscipyをインストールしてもモジュールとして読み込めない。
これはPYTHONPATHの設定の関係で/usr/lib64/が読まれていないためであった。
次の記事に従って解決。
Setting Your PYTHONPATH environment variable (Linux/Unix/OsX)scipher.wordpress.com
やっと動いたのでこれでpythonがラボのオフィシャル言語(仮)になった。
ちなみに最近はラボのメンバーがプログラミングに手を出しはじめており、AWKをはじめ、Perl、Matlab、Mathematicaなどの言語が使われている。何を使えば一番いいのかは分からないが、面白くなってきたなあと思う。
久々に少々長いプログラムを書いた
論文を投稿したのだが、1ヶ月前に4人のレフェリー全員から好意的な結果が返ってきた。誰もrejectを示唆しなかったのはこれまでの経験でも殆ど無いし嬉しい。
とはいうものの、いずれのコメントでも修正点や質問が沢山あり、答えにくい質問も含まれていた。ちゃんとしたデータを出して認めてもらうことが必要であり、ないがしろにすると蹴られる。
大体の問題はボスの知識と1ヶ月に渡る文献調査とGaussian09を使った簡単な計算で解決されたのだが、質問のうちの1つがどうしても既存の文献だとサポートしきれず、新しくプログラムを書き下ろして解析することとなった。結果的に全部で1000行弱のものになった。
今回あったことと雑感
・今まではずっとPython 2系を使って書いてきたのだが、流石にサポートの問題とかもあるため、前々からPython 3に切り替えたいと思っていた。いい機会なので練習がてら使ってみることにした。print文が関数になっており戸惑ったり、rangeをリストとして利用できないなどの点に困ったが、慣れると案外使いやすい。
・初めて最適化アルゴリズムを採用した。この記事(最適化アルゴリズム - sonoshouのまじめなブログ)に従った。webにこういう記事があるありがたさを感じる。最初は焼きなまし法を採用したのだが、確率的に他の不安定状態にうつる箇所があるとどうしても上手く行かなかったため、ステップ数の増加に従ってパラメータの変位が小さくなる点を残してあとは自己流で適当に作った。Local minimumに落ちるのを回避するため、同じ計算を数度繰り返し、直近数回の誤差が100万分の1とかになった時のみ採用するという条件を課した。39次元の変数の最適化を行ったが、この方法だと案外うまくいった。
・自分の不注意によるミスに多く出くわした。特に三角関数の微分で時間の係数を三角関数にかけたとき、ラジアンの変換に使う2πをかけ忘れててとんでもない値が出てた時は間違いに気づくまでに一晩かかった(寝て起きたら気づいた)。
割と楽しかったのでこれからもプログラミングを多用して研究していきたい。
ミネソタ汎関数に分散力補正を入れること等についての雑感
最近になって、ミネソタ汎関数に分散力補正を入れた論文を何報か立て続けに見た。違和感を覚えたのでメモしておきたい。
そもそも分散力補正は開発当時の既存の汎関数(B3LYPなど)が分子間力をうまく取り入れることができないという欠点を補うために開発された方法であり、すでに分子間力をうまく表現できるミネソタ汎関数に追加する必要はないはずである。
(ミネソタ汎関数の分子間力の再現性については下記の論文が分かりやすい
http://pubs.acs.org/doi/abs/10.1021/ar700111a)
おそらく、無理に分散力補正をつけた方法では、分子間力を大きく見積もりすぎて分子を無理やり近づける結果になっていることであろう。構造、エネルギーともにその信頼性に疑問が持たれる。
可能ならば、ベンチマークテストを行って結果を比較したいと思っている。